一国国民每年的劳动,本来就是供给他们每年消费的一切生活必需品和便利品的源泉。(亚当·斯密,《国富论》)
我们将在这一章里阐述,合理的经济计算应该以对时间,具体而言是对劳动时间的计算为基础。这不仅有利于建立公正的社会,而且同样有利于技术的进步。我们将进一步说明,一套按照劳动时间进行产品成本估价的体系不仅仅只是一个美好的理想,它也可以通过现代计算机技术得以实现。在这个说明的过程中,我们将向读者介绍一些关于计算的概念,这些概念与经济的组成有关。
在上一章我们说明了人们如果按照劳动时间取得报酬,就是说人们劳动一小时便得到一小时劳动货币,长此以往,剥削就消灭了。这一巨大的社会利益自然是采用劳动货币的一个理由。它的确是实行社会主义的经典理由——它废除了工资上的压迫并把劳动果实还给劳动者。这样的正义和公平并非这种经济计算方法所带来的唯一好处,它还能促进技术的进步。
很遗憾,人并不能永生。人们在有限的生命中可以生产的产品总和,即社会的财富,取决于他们为了生产其渴望或者需要的产品而被迫花费的时间。人类文明的进步受制于一个时代的经济发展水平。生产其必需品所花费的时间和努力愈大,这个社会就愈贫穷,也就愈加不能维持我们称作文明的娱乐、艺术、文化。所以,用来节约劳动力与劳动时间设备的飞速更新换代正是最近两个世纪以来工业化世界的发展欣欣向荣的根本原因。
时间的节约
任何新技术崛起的基本经济理由是节约劳动力。只有在经济上不断应用这样的发明,人类因此才能被解放从而获得更多的休闲时光或去尝试更加新鲜而复杂的事物。一名社会主义的建设者必须一如既往地寻找节约时间的方法。正如亚当·斯密所说,它是我们的“原币”,一旦被浪费,就意味着永远的失去。只有当社会主义证明自己能更好地节约时间,才能表明其相对资本主义具有优越性。
在资本主义经济中,制造商受利益驱使,尽可能地降低成本,其中就包括工人工资。公司经常采用新技术以便削减劳动力和相应开支。尽管新技术的应用经常与工人的直接利益发生冲突,导致他们失业,但整个社会最终会受益。技术变革所带来利益并没有被平均分配——雇主比雇员获益更多——但是最终,其促进了技术的变革,资本主义正是以此为基础才宣称自己是进步的制度。工会内部一般也接受新技术的应用,只不过要在保证全体工人利益的前提下。
社会主义经济经常批评技术变革,认为其导致失业,而这是一种很幼稚的想法。在这一点上,资本主义需要反思的是其劳动节约型设备的更新换代速度太慢了,因为劳动力被人为压低。
尽管有古希腊的科学和古罗马的工艺,但古希腊人和古罗马人没能创造出一个工业社会。历史学家经过长期争论认为,其原因在于奴隶制。当所有的工业生产都由奴隶来进行时,对劳动力成本的理性计算就显得多此一举。一个奴隶并非按小时付给报酬,所以主人就没有计算劳动时间的动力。而没有这样的计算,节约劳动时间概念就更无从谈起。所以,比方说,尽管罗马人知道水车,却从未进一步广泛地应用机械动力。(White, 1962)
资本主义相对于奴隶制是一个明显的进步。资本家按小时付给劳动力工钱,因此不愿意浪费。他通过对工作时间和强度的研究来检验自己花钱是否值得。但是,他仍以低廉的价格购买劳动力,否则他就得不到利润。这里有一个悖论:价格便宜的东西永远不会真正被珍惜。工资越低,利润就越高;但是工资低的时候,雇主就浪费得起劳动力。在理性方面,资本家比奴隶主更高级,但仅仅是高级一点而已。
英国铁路是个技术奇迹,宽广笔直的铁轨穿越大地
隧道穿越高山,路堤高架桥横跨峡谷
如今铁路的印记在这片土地上依旧存在
这是创造巨大财富的商业之路
这是日不落帝国的供给之路
这是无处不在的光明之路①
……毫无疑问,铁轨将为新千年的到来做准备,像曾经的罗马帝国的道路和水利工程一样。用着过去罗马奴隶修水利时使用的工具,劳工们和“航海家们”修建了铁路。铁路是强健的肌肉用凿子和铲子建成的。两千年里的一个伟大的技术进步是由中国人发明的独轮手推车。工人们使用它,而奴隶们则不使用它。②
铁路是机器时代的产物。但是没人超越史蒂芬孙和布鲁奈尔的智慧,去设计蒸汽动力的挖掘机械。由于报酬上的奴役(雇佣劳动者)相对更便宜,所以就用不着那么麻烦了。
在本世纪的英国码头(本书作于二十世纪八十年代——译者注),码头工人仍然用着自中世纪就没有改变过的技术去装卸货物。工人们按天雇佣,做着奴隶的工作,却没有奴隶制下的安全。要想让资本家阶级意识到在推土机、重型挖掘设备和集装箱化上的投资是划算的,就需要有充分就业、强大的工会和更好的工资待遇。
上面的例子都是些体力工人,通常被认为是工人阶级受剥削最深的一群人。类似情况也存在于许多低工资的血汗工作中——服装制造,玩具制造等等。在这些领域,生产技术停滞,创新的热情也不高。我们可以得出一个普遍的规律,工资越低,雇主就越不愿与实现现代化。 我们可以用表3.1中的例子说明这个规律。
表3.1 两种挖沟的方法

假设:
劳动创造的价值 7.53英镑每小时
工资率 3英镑每小时
表中显示的是用两种方法在一条路上挖沟的相对成本分别是多少。用旧方法,承包人雇佣两个人,每个人在一周内分别劳动50小时。除此之外,他还需要租一台压缩机和两个风钻。它们是用来进行路面破碎,然后让工人用铲子掘土。压缩机和风钻的损耗加上压缩机所耗费的燃料,共计达到100小时的劳动。使用现代技术,承包人只需一台挖掘机并雇佣一个人,工作50小时就可完成。这里,挖掘机和燃料的消耗共计为125小时的劳动时间。现代技术仅仅需要175小时的直接和间接的劳动就可完成这项工作,而旧技术则需要200小时。
假设在1987年的英国,一个小时的劳动所创造的产品的售价为7.53英镑,而一个小时的劳动报酬为3英镑。如果我们计算一下两种技术所耗费的货币成本,我们会发现一个颠倒的结果,旧方法更便宜。因为劳动力更廉价,劳动力密集的技术显得成本更低,这就导致资本家浪费人类劳动。
计算机工业中也能找到很贴切的例子。20世纪50年代,IBM开发了高度自动化的机器去为他们的计算机构建核心存储器。随着需求的增长,他们的工厂变得越来越自动化。到了1965年,他们甚至要为制造电脑的机器开设了一条全新的生产线。即便如此,计算机的生产仍然跟不上需求。
形势变得更严重了。金士顿(Kingston)新上任的经理曾经在日本待过几年。他提出,东方国家的工人有足够灵巧的双手和耐心,可以找他们手工制作磁芯板。他带着一包包磁芯,线圈和砂心框去了日本。十天后,他带着手工磁芯板从日本回来了,质量和金士顿工厂里的自动送丝器制造的一样好。这个工作又慢又乏味,但是东方工人的工资是如此之低,以致于生产费用实际上低于金士顿的全自动生产。(Pugh et al., 1991, p. 209)
对于苏联七八十年代针对价格和工资体制的改革,有一种批评是:低工资会导致同样的劳动的浪费。在苏联,工资保持低水平,居民收入的一大部分来自丰厚的住房补贴和公共服务。雇人的企业不给人们支付这些服务的费用。改革派支持价格和工资体制的变革,以提高服务方面的支出,而工资相应增长则可补偿这一部分。他们宣称,更高的工资会起到创新激励的作用。
这一论证是可行的,但还远远不够。因为工资,也就是付给劳动的价格而不是劳动时间本身,被当作了成本,所以问题出现了。这意味着,一切不同生产技术之间的成本比较,其结果都会受到工资水平的影响。如果我们将工资纳入成本进行计算,我们就无法抛开收入分配而对经济效率进行衡量。为了避免这种情况,我们需要找到一些客观的方法衡量产品生产所用的劳动量。这说起来容易做起来难。
客观的社会核算
厂商依据市场价格变化确定成本。这为厂商选择更廉价生产方式提供了某种理性基础,即使这样的选择会更多地偏向浪费劳动的工艺。如果想找到关于成本方面更客观的信息源的话,我们需要一个独立于市场之外的信息收集系统。这时就需要引入计算机技术了。我们需要一个计算机化的信息系统,它能准确估算不同工艺所耗费的劳动时间并将这一数据提供给产品工程师。
在资本主义国家,市场价格被看作成本的指示器,但这有一定的盲目性。一位艺术家死时分无分文,而几十年后他的作品几经转手却已价值百万;股票市场被突如其来的恐慌所袭击,仅仅几个小时,股票市值就蒸发了数百亿;因为价格过低,农民不得不销毁自家庄稼。走过英国或美国的贫民区,你会看到人们憔悴的面庞和发育不良的身躯,因为食品价格对他们来说太贵了。
市场价格是供给和需求两方的玩物。需求不依赖于人们的实际需要,而依赖于支付的能力和意愿。这意味着财富的分配、一时的心血来潮和时尚潮流都会影响需求。供给受制于更加单调的约束:用于进行生产的资源。
一幅凡高的新作品需要凡高自己来创作,但凡高又在哪里呢?所以,凡高原创作品的供给不可能再增加。而这些现存的原创作品由于承载了人们对这位作家的无限遐想,其价格就被那些富人的荒唐和虚荣心而无限推高。
西红柿的供给依赖于劳动、土地、阳光、水、温室、油等等。它们的生产成本取决于农业技术和投入的成本。它们的供给受制于客观的约束,这限制了它们的价格。
我们永远不能合理估算达芬奇现在一幅作品的创作成本,但在社会主义经济下应该可以对不同的产品的客观费用做出一些估计。原则上,我们可以对任何广泛使用的资源的费用做出估计。在工业社会,我们可以根据生产中消耗的产能给商品定价。如果由于环境原因,工业生产面临着全面的产能限制,那么也许就该换一种产品定价方法了。我们支持用劳动时间作为计算的基本单位,因为我们认为社会是人的社会,至少从目前来看,人们怎样生活至少比任何一种自然资源都重要。我们会在第五章回过头来讨论基于环境的考量而反对过分依赖基于时间的估算方法。
定义劳动内容
为了按照劳动去估算成本,我们需要给一个产品的劳动内容下定义。如果我们想知道一个西红柿的劳动内容,就不能只计算农民照看和采摘它一共花费了多少秒。我们还要将间接劳动考虑在内:人们建造培育西红柿的温室所花费的劳动;石油工人生产温室所需燃料的劳动,等等。但我们似乎陷入了一个循环的矛盾中:要想知道一种产品的劳动内容,我们就还要知道另外好几种产品的劳动内容。
为了解决这个复杂的相互依赖的问题,我们需要的一个投入-产出表。它记录着一些部门的产出是如何被用作另一些部门的投入的。在表3.2中给出的例子中,食品部门每周消耗2000桶原油,雇佣2000名工人,生产40000条面包。石油部门每周雇佣1000名工人,耗费500桶原油,生产出2000桶原油。这个简单的经济体净生产40000条面包和500桶原油,作为3000名劳动者食品和燃料。
表3.2:一个简单的投入产出系统
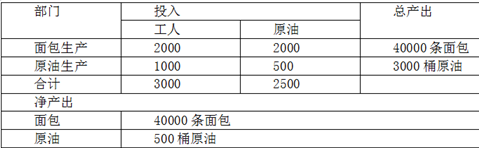
表3.2所展示的关系可以被用来计算原油和面包中的劳动内容。
先来看面包。我们希望发现,生产一条面包需要多少个“人-周”的劳动,。
一个人劳动一周,也就是说,创造了一个人一周的价值。我们从表中可以知道:
40000条面包的价值=2000人-周+2000桶原油的价值(3.1)。
也就是说,面包生产中创造的价值,等于这项生产中直接劳动,加上由原油的投入所代表的间接劳动。为了说明面包中包含了多少个“人-周”的价值,式(3.1)可以被化为一下形式:
一条面包的价值=(2000+2000×原油价值)/40000(3.2)
因此,按照劳动,如果我们知道原油的价值,我们就可以算出上面要求出的价值。从表中我们可以看出:
3000桶原油的价值=1000人-周+500条面包的价值(3.3)
所以,2500桶原油价值1000人-周,而一条面包的价值一定值1【人-周】的0.4或者五分之二。现在我们可以算出面包的价值:
面包的价值=1.40/20=0.07人-周
所以最终结果是,一条面包和一桶原油的劳动价值分别是0.07和0.4人-周。③
规模问题
在《可行的社会主义经济》(1983)一书中,亚力克·诺夫强调了现代经济的规模的重要性。他说苏联经济包括1200万种产品,并且引用了O·安东诺夫的估计:为乌克兰起草一个完整且平衡的计划会耗费全世界人口超过1000万年的劳动。
同样的争论也适用于计算劳动价值。投入产出表格里的玩具模型方程式的求解是一回事,而解开一个由1200万个方程式组成的联立方程组却是另一回事。但是,仅仅指出计算一个大经济体的劳动价值是复杂的这一事实是不够的,我们还必须知道它到底有多复杂。诺夫引证的例子让我们感觉这是一种庞大的难以处理的复杂事物,而这种印象似乎关闭了进一步研究的大门(我们应该指出,诺夫绝不是唯一做出这种结论的人。这种论点在反社会主义者中经常可以见到。我们举出诺夫的例子来证明即便是左倾的经济学家对社会主义计划的复杂性也往往束手无策)。而我们需要描述一套法则,这些法则能决定为复杂程度不同的经济所做的劳动价值计算需要耗费的时间。
用人工方法准备这个方案(或者计算劳动价值)几乎是不可能的,但是这并不意味着用计算机也不行。为了着手做这件事,我们需要在将要制定的经济规模和所需的计算机工作时间之间建立数量关系。计算机科学的其中一个分支——复杂性理论所研究的,正是进行计算所需要的时间。
复杂性的理念
复杂性理论解决完成计算所需要的不连续步骤数量的问题。这些不连续步骤大体上要与在计算机程序中执行的指令一致。举一个例子来考虑这个问题。
给你99张卡片。每张卡片上分别印着1到99这些数字。卡片的顺序是任意的。你需要把他们按升序排列。你会怎么做?有一种解决方案需要应用下面所述方法。
(1)把第一张卡片与第二张比较。如果第一个比第二个大,则交换它们的次序。
(2)用第二、三、四对卡片去重复步骤一,直到你到达底部。
(3)如果你发现这一叠卡片的顺序是正确的,那么你可以停下来了。否则,你还要重新进行第一步。
用这种方法给卡片排序会用多长时间呢?这取决于卡片原有的顺序。最好的情况是,卡片一开始就是升序排列的,这样进行一遍98次的比较就足够了。最坏的情况是,卡片一开始是降序排列的。你现在需要将顺序颠倒过来。你看到的第一张卡片上的数字是99。第一步将它移动到第二张,然后第一步会被重复直到我们翻到这一叠的最后一张。每一次,印有99的卡片都会被移动一个位置。最终,经历98次重复,它到达了底部。
于是,一次对这叠卡片的单程扫描会把一张卡片移动到正确的位置。开始时,有99张卡片都处于错误的位置。所以,我们需要对折叠卡片做99次重复扫描。最坏的情况下,操作的次数将会是n²(n表示卡片的数量)。
这里有一个更好的方法。
(1)依据卡片的末位数字是0,1,2,……9,将这一叠卡片分成10组。
(2)将各组按照0到9的顺序排列,形成新的一叠。
(3)从叠的底部开始,依据每张卡片的第一位数字,将它再次分成10组。
(4)重复步骤2。这一叠卡片就被整理好了。
使用第二种方法,我们只需要对每一张卡片看两次。操作的次数也就是2n(n表示卡片的数量)。相比于前一种,这显然是一个更快的方法。我们说它需要耗费时间量级为n。
时间量级为n的问题比时间量级为n²的问题要容易。最糟糕的问题是需要指数级的步骤才能解决的问题。指数问题通常被认为实际估算起来很复杂,除非n是一个很小的数字。
在考察一个经济计划问题和用计算机进行必要计算的可行性的时候,我们需要确定涉及到的估算的时间量级和输入数据的规模(n)。
简化劳动价值问题
让我们回到在一个经济体内计算各种产品的劳动价值这个问题。生产的条件可以体现为一个投入产出表。从这个表格中我们可以得出一组方程,就像上面的例子一样。理论上,这些方程无疑是可解的——我们所列的方程数和我们要解的未知的劳动价值是相同的。问题在于,这个系统实际上是否可解。
解决这些联立方程的标准方法是高斯消元法。④这和学校教课书里的方法是一样的。这种方法可以在与方程组内方程数量的立方成比例的运行时间中得出精确解。⑤
让我们假定,在要进行计划的经济中,不同的产出类型是百万(10^6)量级。这种情况下,高斯消元法应用到投入产出表格里,将需要(10^6)的立方次也就是10^18次迭代,每次迭代需要10次原始的计算机指令。
假如我们能在一台现代的日本巨型计算机例如富士通VP200或者日立S810/20上去解决这个问题,我们需要用多长时间呢?这些机器在处理大规模数据时,可以在一秒内进行大约2亿次计算。(见Lubeck et al., 1985)⑥。所以,计算经济中所有劳动价值所需的时间将会是500亿秒或者16000年。这显然太慢了。(富士通VP-200是1983年出的超级计算机,速度不过400 MFLOPS。一直到1990年,全球最快的超级计算机也只有23.2 GFLOPS(NECSX-3/44R,1990)。计算机技术一直在进步,到了2013年,全球最快的超级计算机是中国的天河二号,速度达到33.86 PFLOPS,即每秒3.39亿亿次双精度浮点运算。对于文中列举的计算量,1983年的超级计算机要500亿秒才能完成,三十年后的超级计算机则只需250秒左右。——译者注)
当一个人遇到这种量级问题时,常常把任务重新划分成不同阶段。在实践中,一个经济的投入产出表格多半会是空白。在现实中,每种产品平均只有数十个最多数百个投入,而不是一百万个。这使得用一列向量而不是一个矩阵来表示这个系统会更合算。其结果是,我们可以走捷径得出结果——使用另一种方法,即逐次近似计算法。
这个想法是,作为第一个近似值,我们忽略生产过程中的除了直接耗费的劳动之外的所有投入。这给了我们第一个每种产品的劳动价值的近似估计值。这将是一个低估值,因为我们忽略了生产过程中的非劳动性投入。为了得出第二个近似值,我们在第一阶段中计算的劳动价值的基础上添加了非劳动性投入。这将会使我们向真正的劳动价值又接近一步。重复应用这种处理过程,将使我们得到所需要的精确度。如果一种平均产品的价值来源于直接的劳动投入,那么围绕我们的近似值的每一次迭代过程都会给我们的答案增加一位二进制有效数字。一个精确到四位十进制有效数字的答案(比市场可以得到的更精确)将需要在求解过程中进行15次迭代 。
这种算法⑦的时间顺序的复杂性,与每件产品中投入的时间的平均值的数量成比例。根据我们原先的假设,这将可以在超级计算机上用几分钟完成,而不是高斯消元法需要的几千年。⑧
高科技和中等技术的解决方法
对整个经济的劳动价值的计算,在今天使用现代超级计算机的情况下,在几分钟内就可以完成。这类计算机价格很贵,但还可以接受。它们已经被广泛用于天气预报、自动化武器设计、石油勘探和核物理研究。给国家计划局和气象局同样的计算能力并非不合理。直至最近,超级计算机技术已经为少数国家所掌握,主要的是美国和日本。英国通过使用高度并发的处理器现在已经拥有了生产有这种机器的能力;爱丁堡大学正在研制一台每秒计算100亿次的机器。截止1988年,苏联有数项计划正在开发类似的超级计算机,但是似乎没有投入批量生产的。(见Wolcott and Goodman, 1988)
然而,值得指出的是,其实用相当低水平的技术就能够取得本质上相同的结果。我们将概述如何实现它。
中等技术方法需要四个组成部分。第一个组成部分是文字电视广播,如熟悉的英国公共商业电视,像Cefax 和Oracle这些。它们是用少量电视频道的带宽就可以传递新闻、体育、前期等数字信息的公共信息系统。第二个组成部分是公共电话网络。第三个组成部分是配有接收文字电视广播的个人计算机,现在每台总价约几百英镑。第四个组成部分是零售业中统一的产品编码系统。统一的产品编码就是几乎所有能买到的产品所带有的条形码上的数字。
除了规模极小的公司外,在个人计算机上使用电子表格程序包进行成本分析已经几乎成为标准实践。在我们假设的社会主义经济中,每个生产单位都用一个这样的程序包来建立其生产过程的模型。这个电子数据表格模型将被填入上周所使用的劳动量,其他各项投入以及总产出。
在有了各项投入的劳动价值最新数据的情况下,这个电子数据表能够迅速地计算出产出的劳动价值。
从哪得到最新的劳动价值呢?它们会被公共广播机构在文字电视广播上持续不断地广播。和以前一样,我们假设有一百万种产品,文字电视广播能够每二十分钟广播一次修正后的劳动价值。产品会通过统一的产品编码被识别。个人电脑侦听并更新电子数据表模型,以回应任何广播的劳动价值的变化。
如果出于某种原因某个工作地点的个人计算机认定当地的劳动价值变化了,那么它将会提醒中心的文字电视广播的计算机并通知这个变化。这类改变或者是由于当地生产技术的一些改变,亦或是由于某种投入品价值改变的广播。整个系统将会像一台分布式的超级计算机一样,不停地通过逐次逼近法求劳动价值。
尽管使用的只是便宜简单的技术,上述方法比一台中央高级计算机更有优势。它不仅进行计算,而且进行数据收集。众所周知,数据收集是任何计划系统中最困难的部分。其次,它将是一个更加健全的系统。如果一些小计算机发生故障,其中一些劳动价值的数据会过时,但整个系统会幸免于难。唯一易受破坏的点是中心文字广播电视系统,但它比中央超级计算机便宜得多,因此可以用备份机器来进行复制。
使用这个发布式计算系统,每个生产单位都能用得到它计算的各种备选生产方案的社会劳动成本。这些数据,即便不是按分钟,也是按小时进行更新。这一系统更新数据的速度,比资本主义市场快太多了。
注释
① Gaston, P., ‘Navigator’, on Rum, Sodomy and the Lash, The Pogues, Stiff Records.
② 在黑死病以后,由于劳动力的短缺,独轮手推车被介绍到欧洲。
③ 这显然是一个非常简单的投入产出表,只有两种投入和两种产出,而真实的经济中会有成千上万种商品。但无论经济的规模如何,数学方法都是一样的。从投入产出表中可以得到如下形式的线性方程:
第三章公式
Li 表示第i个行业中使用的直接劳动量。Iij是第i个行业使用的第j个行业的产出品的量,vi表示第i行业产品的单位劳动量;而Qi表示第i行业的总产出。我们有n个等式和n个未知数:vi。因为独立等式的数量和未知数的数量相等,所以从原则上讲,我们可以解出vi。而这些未知数正是我们在寻求的所有产品的劳动内容。
④ 我们从n个等式n个未知数开始。通过将第n个等式乘以合适的倍数,可以将其减少为n-1个等式和n-1个未知数。然后,迭代执行这一步骤,我们最终得到1个等式一个未知数。这一等式是直接可解的。然后,我们再吧这个值代回到之前的2个方程2个未知数的系统,如此循环往复。
⑤ 背后的原理并不复杂。要消去任一变量,我们必须执行n(n-1)次乘法运算。有n个变量要消,因此问题的复杂度的量级为n的立方。
⑥计算机技术从八十年代中期以来已经取得了很大的进步,应该牢记这一点。到90年代中期,制造商希望实现能够进行每秒十万亿次运算的机器。
⑦ “算法”一词是al-Kowarizimi这一名字的变体。al-Kowarizimi是九世纪波斯数学家。他写过一本书,普及了使用印度十进制系统进行的基本算术。现在的“算术”这一术语就是在这本书传入欧洲时,被为“算法”(algorithmics)的。它与使用算盘和罗马数字系统的算术“arithmetics”不同。Algorithmics的关键点是使用一组简单的规则和基本的加法和乘法表。把这些规则和加法乘法表背下来,就能进行任意大小数字的计算。扩展到其他数学问题,算法就是不需要太高智慧,能一步一步执行下来,得到某种结果的过程。长除法或者取平方根时就会用到简单的算法。这种算法的正式名称是递归过程,使用这种方法,能够在有限数目的步骤内能得到问题的答案。任何能够表达为算法的问题都能被机器求解。
⑧ Hodgson (1984, 的。所以正如上面证明过的那样,更好的运用数据结构,可以大幅度地减少复杂度。
- 作者:保罗•科克肖特、阿林•科特尔
- 翻译:尘沙
- 校对:黑夜里的牛
